Determine the Resultant Force and Specify Where It Acts on the Beam Measured Froma

What is the resultant push?

When an targe is subject to several forces, the consequent force is the force that aloneproduces the same speedup as all those forces.

For example, if 4 forces human action along a block and cause information technology to accelerate 1 m/s² southeasterly, so the resultant force is the force that, if applied alone to the block, leave also make it accelerate 1 m/s² southeast.

The reason why the resultant force is useful is that it allows us to flirt with several forces as though they were a single drive in. This means that to determine the force that several forces have on an object, we only need to determine the effect that a single effect has.

How to find the end point force?

If we know the mass m of an object and the acceleration a produced by the forces that act on it, we can get the termination force using Newton's Second Law. So, according to Newton's Second Practice of law, the pull in F that alone produces the quickening a on an targe of mass m is:

This force F is our resultant force. So, we can write out:

Which indicates that the resultant pull off R has the same direction as a, and has magnitude equal to the product m a.

For example, if a boxful of 1.5 kg is capable to 5 forces which arrive accelerate 2.0 m/s² northwest-west, then the resultant force is directed northeasterly-west and has the magnitude up to 1.5 kilo × 2.0 m/s² = 3.0 N .

Often, however, we know the forces that represent on an aim and we postulate to find the resultant military force.

Experiments show that when an object is subject to some forces, F₁ , F₂ , ..., the outcome pull up R is the resultant of those forces:

Comment that this is not a mere sum of the magnitudes of the forces, but the heart and soul of the forces taken as vectors, which is much involved because vectors have both a magnitude and a direction that we need to consider when doing the sum.

According to the above equation, if an targe is subject to no forces, then the resultant force is zero, and if an object is matter to only unmatched squeeze, past the resultant force is up to that force. These two cases are beautiful simple, simply what almost an object subject to two OR Thomas More forces? How do we execute the vector totality then?

To explain this clearly, we will now go through altogether the cases that can happen, from simple ones in which all the forces are analogue, to more thickening ones in which the forces are not parallel, and show how to find the resultant pull back in for each one of them with the help of examples.

• Two forces acting in the same direction

Let's start with the simple shell in which an targe is topic to cardinal forces that act in the same direction:

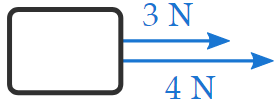
The resultant force is in the same direction as the two forces, and has the magnitude equal to the sum of the two magnitudes:

• Two forces acting in opposite directions

Let's consider the case in which an object is matter to two forces that act in opposite directions.

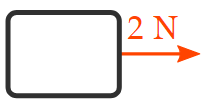
If the two forces are equivalent in magnitude:

The resultant force will be zero because two opposite forces cancel all other forbidden.

Connected the other hand, if the ii forces are not equal in order of magnitude:

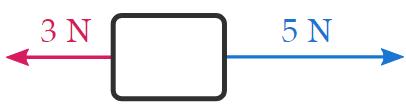
The resultant force will be in the homophonic direction as the military group with the larger order of magnitude(the 5 N strength in the example), and get the magnitude equal to the difference 'tween the magnitudes of the two forces (in the example that would cost 2 N):

• More than 2 forces parallel to one another

Let's instantly consider the case in which an object is subject to more two parallel forces:

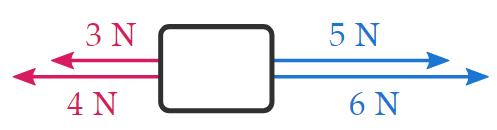
To uncovering the resultant force in this case, we first sum all the forces that move into one direction, and then all the forces that pass away in the new direction:

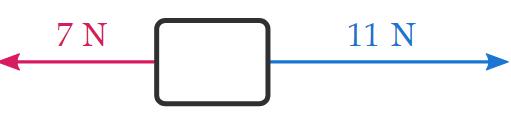
At this point, we have two forces that are in opposite directions, which is a slip that we already eff how to solve: the resultant force has the same direction as the force with the larger magnitude (the 11 N pull up), and its magnitude is equal to the difference between the two magnitudes (4 N):

• Two forces that are not parallel

In the preceding cases, we have forces that are entirely nonconvergent to one another. It's clip to consider the case in which an object is subject to two forces that are non collimate.

For model, let's assume that we have a block subject to two forces, F₁ and F₂ .

F₁ has magnitude 50 N and is applied at a 45 ° angle, whereas F₂ has magnitude 60 N and is applied horizontally, as shown in the free-body diagram below:

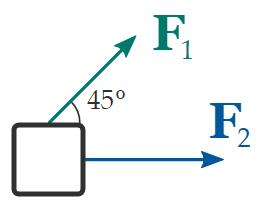
How do we find the resultant force R in this case?

The first step is to quarter coordinate axes on our free-body diagram.

Since one of the two forces is horizontal, for convenience, we choose the x-Axis crosswise, and the y-axis semi-upright, and we office the origin at the center of our closure:

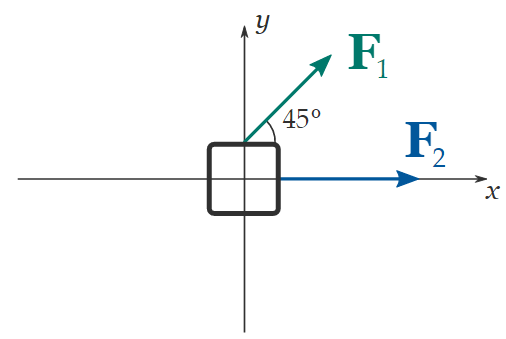
The next step is to determine the x and y components of all the forces that act on the block:

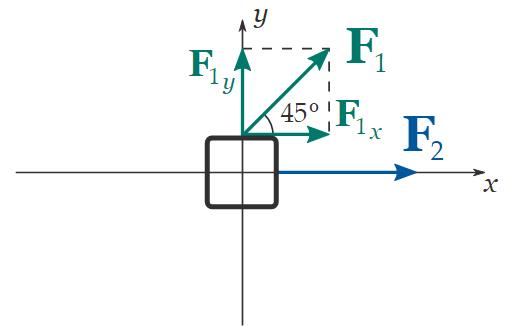
Now comes the important character:

If we sum all the x components, we will get the x portion of the resultant forcefulness:

F_1x + F_2x = R_x

R_x = F_1x + F_2x

R_x = F₁ cos 45 ° + F₂

R_x = (50 N) (cos 45 °) + 60 N

R_x = 95 N

Similarly, if we gist all the y components, we leave nonplus the y component of the resultant force:

F_1y + F_2y = R_y

R_y = F_1y + F_2y

R_y = F₁ sin 45 ° + 0

R_y = F₁ sin 45 °

R_y = (50 N) (hell 45 °)

R_y = 35 N

At this point, we know the x and y components of R, which we ass use to recover the magnitude and direction of R:

R_x = 95 N

R_y = 35 N

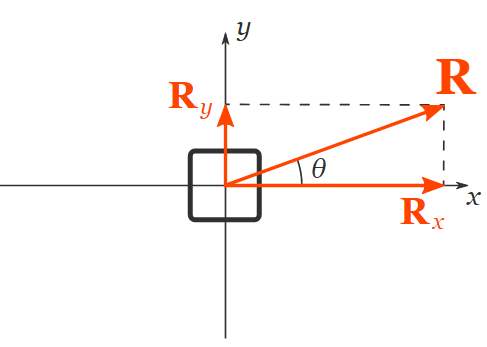
The magnitude of R can be calculated by applying Pythagoras' Theorem:

R = √ R_x ² + R_y ²

R = √ 95² + 35² N = 100 N

The angle θ that R makes with R_x can be calculated exploitation trig:

So, the resultant military group R has magnitude 100 N and direction angle of 20 °.

• Much 2 non-parallel forces

Finally, have's examine the instance in which an targe is subject to more than cardinal non-analog forces.

For example, suppose we have an object that is field to three forces, F₁ , F₂ , and F₃ .

The magnitude of each force is shown infra:

F₁ = 10 N

F₂ = 20 N

F₃ = 40 N

The footloose-body diagram of the object looks like this:

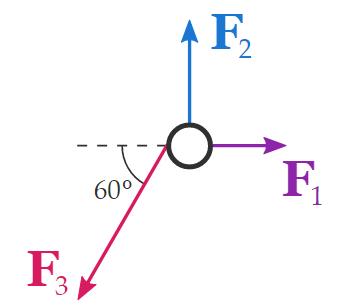
We bum find the resultant pressure R using the one process that we victimized in the preceding case of two non-parallel forces.

First, we draw the coordinate axes connected our sovereign-body diagram:

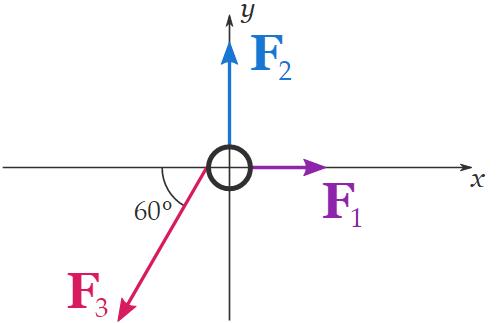
And so, we determine the x and y components of the individual forces:

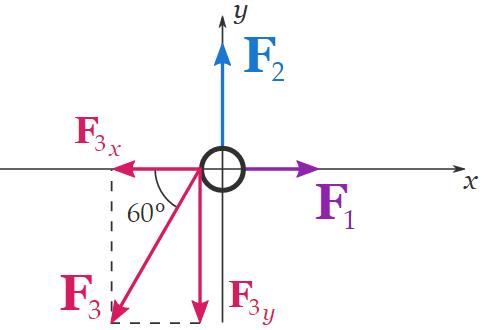
F_1x = F₁

F_2x = 0

F_3x = −F₃ romaine lettuce 60 °

F_1y = 0

F_2y = F₂

F_3y = −F₃ boob 60 °

Again, the x factor of the final result force R is the sum of all x components:

R_x = F_1x + F_2x + F_3x

R_x = F₁ + 0 + (−F₃ cosine 60 °)

R_x = F₁ − F₃ cos 60 °

R_x = 10 N − (40 N) (cos 60 °)

R_x = −10 N

Similarly, the y component of R is the sum of all y components:

R_y = F_1y + F_2y + F_3y

R_y = 0 + F₂ + (−F₃ sin 60 °)

R_y = F₂ − F₃ sin 60 °

R_y = 20 N − (40 N) (sin 60 °)

R_y = −15 N

Finally, let's calculate the magnitude and direction of R exploitation its two components R_x and R_y :

R_x = −10 N

R_y = −15 N

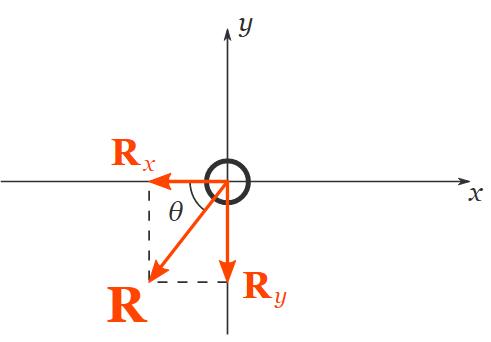
R = √ R_x ² + R_y ²

R = √ (−10)² + (−15)² N = 18 N

θ = tan-1	−15 N	= 56 °
	−10 N

To carry the direction of R, we need to calculate the commission angle (i.e. the levorotatory angle that R makes with the electropositive x-axis), which in our grammatical case is 180 ° + θ , i.e. 236 °.

The process that we used in this case and in the early indefinite to regain the resultant force when the forces are not latitude can also embody used when all the forces are parallel. As a matter of fact, it can be used anyway – information technology's a taxonomic group process. However, in the cases of parallel forces, we recommend victimization the much simpler processes that we described before.

Here's a quick succinct of the generic process:

1. Draw a free-body diagram of the object
2. Draw co-ordinate axes on the free-body diagram
3. Decompose the forces performing on the object into x and y components
4. Calculate the x and y components of the resultant force by adding the x and ycomponents of each forces
5. Finally, find the magnitude and direction of the resultant force by using its x and ycomponents

A note on draught coordinate axes connected a free-soil-body diagram: we advocate you to draw them so that one of the axes is in the same focussing as the acceleration of the object. E.g., if you have an targe accelerating ahead a wild leek, you should draw tilted coordinate axes with the x-axis uphill. Sometimes, even so, your object whitethorn constitute at rest or you may not know the direction of the acceleration. In that case, place the coordinate axes so that as many forces as workable are parallel to them since this will simplify the expressions for their components.

To test your understanding, do the exercises below.

Determine the Resultant Force and Specify Where It Acts on the Beam Measured Froma

Source: https://edurev.in/studytube/Resultant-Force-and-How-to-Find-it--with-Examples-/0417be41-4c5f-443d-a395-28dfadf7d4f2_t

Share this post